
Objectives: Examine how Darcy’s law changes when transitioning to radial coordinates.
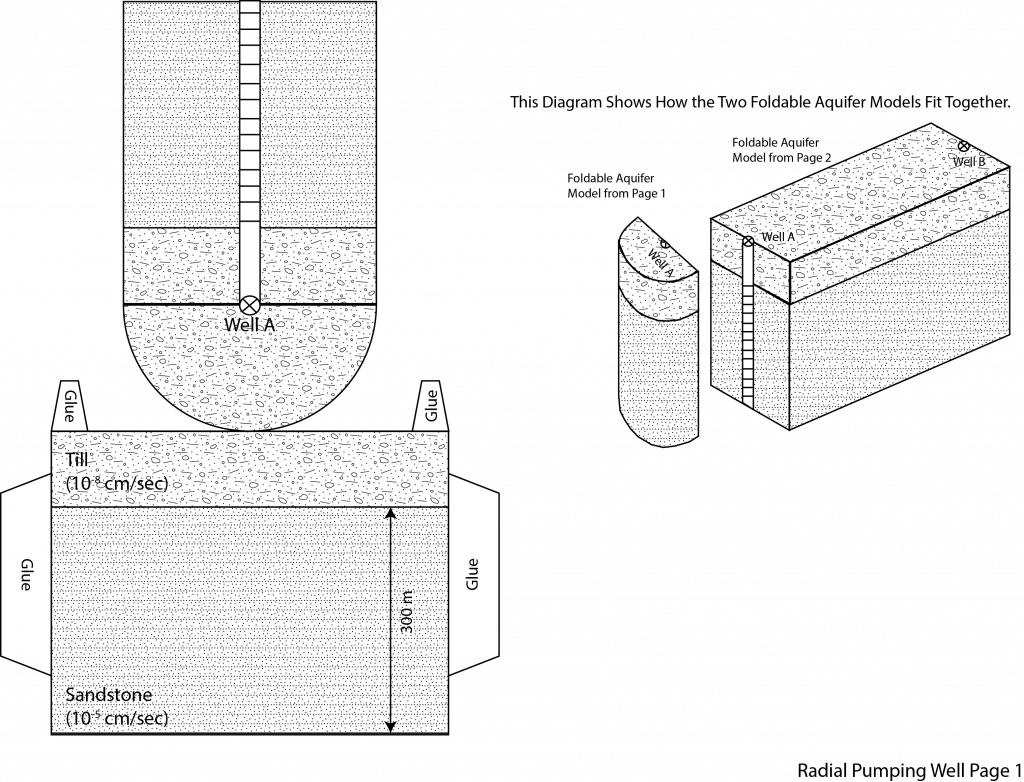
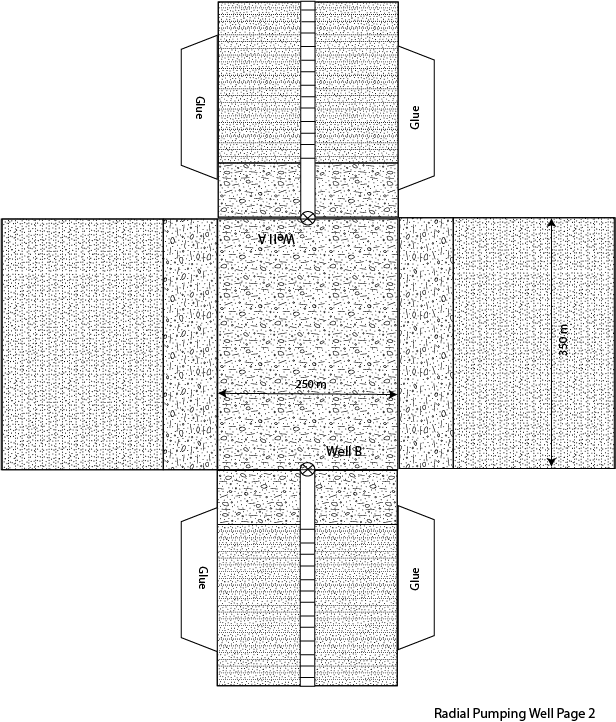
1. When a well is being pumped in a homogenous aquifer it is a lot easier to quantify drawdown at a given distance away from the well using radial coordinates. This is because draw down away from the well is the same at any distance rx away from the well. As a result, when dealing with a well that is being pumped we need to modify Darcy’s law from cartesian coordinates to radial coordinate (see equations below). In the following problem we are going to assume that well A is a pumping well that has been pumping for a long time. As a result, the water level is not changing with time and we can consider this a steady state problem. The water levels in well A and B are given in the table below. We are going to assume that the wells have a radius of 10 cm. Using the foldable aquifer model address the following problems.
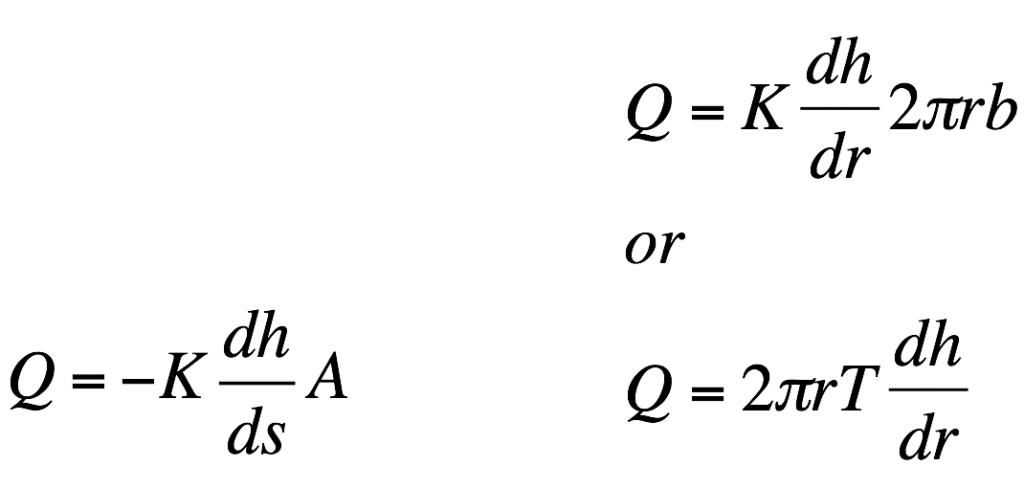
| Well | Water Level (m) |
| Well A | 385 |
| Well B | 395 |
A. Quantify the hydraulic gradient between well A and well B.
B. Describe what the area term in Darcy’s law represents in the problem below, considering water is flowing between well A and well B.
C. Determine the pumping rate in m3/day that is necessary at well A to produce the drawdown described above.

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
